Independence Testing Power vs. Dimension

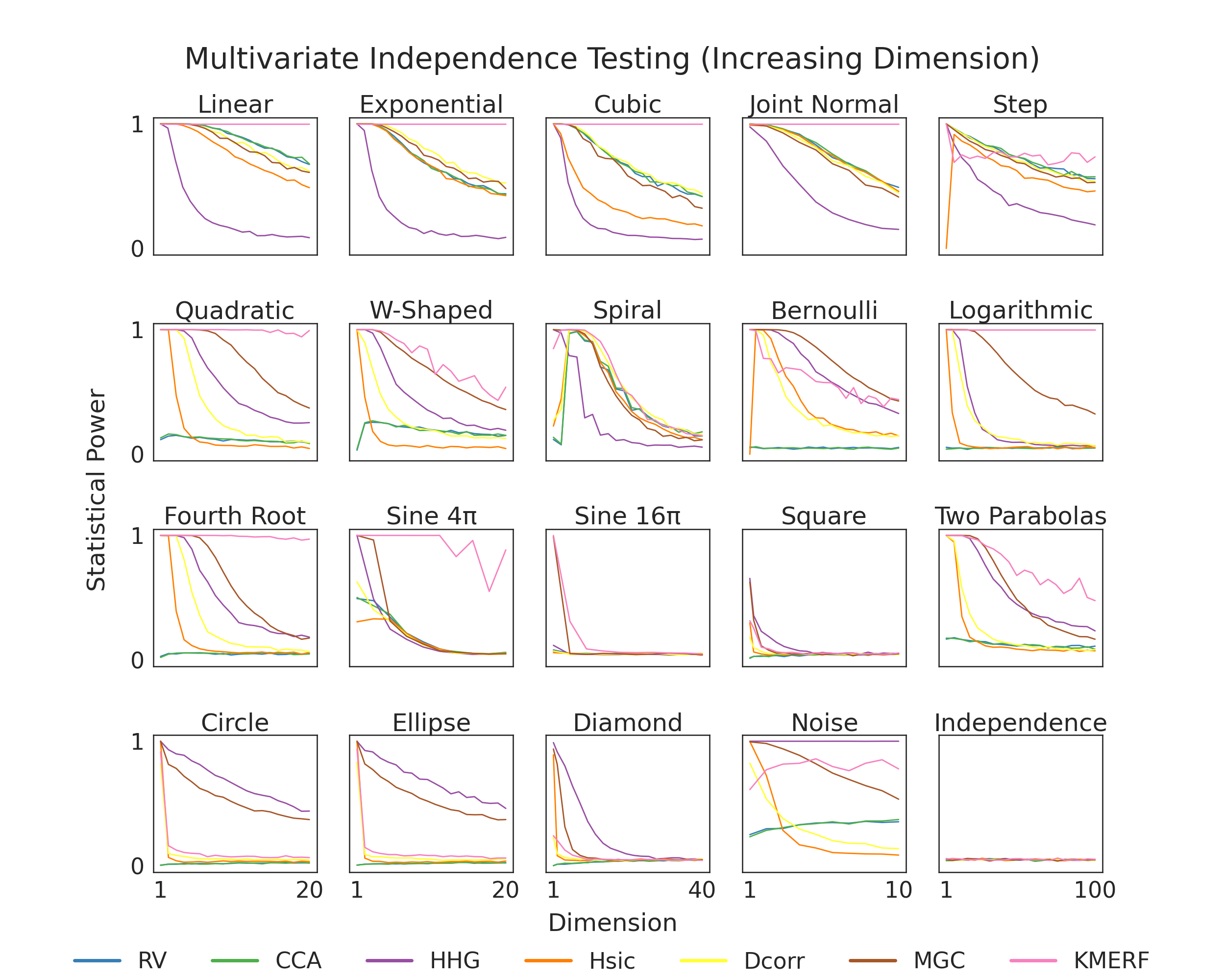
Here, we show finite testing power comparisons between the various tests within hyppo. Because of the struggles of high dimensional data, we expect that in most cases, that finite testing power decreases as dimension increases. Tests that converge to 0 slower have higher finite testing power and are likely better to use for your use case. The simulation in the bottom right is used so that we know that we are properly controlling for type I error, which is important becase otherwise the test would be invalid (power = alpha-level = 0.05).

import os
import sys

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from hyppo.independence import INDEP_TESTS
from hyppo.tools import SIMULATIONS, power
from joblib import Parallel, delayed

sys.path.append(os.path.realpath(".."))

# make plots look pretty
sns.set(color_codes=True, style="white", context="talk", font_scale=2)
PALETTE = sns.color_palette("Set1")
sns.set_palette(PALETTE[1:])

# constants
POWER_REPS = 5

# simulation titles
SIM_TITLES = [
    "Linear",
    "Exponential",
    "Cubic",
    "Joint Normal",
    "Step",
    "Quadratic",
    "W-Shaped",
    "Spiral",
    "Bernoulli",
    "Logarithmic",
    "Fourth Root",
    "Sine 4\u03C0",
    "Sine 16\u03C0",
    "Square",
    "Two Parabolas",
    "Circle",
    "Ellipse",
    "Diamond",
    "Noise",
    "Independence",
]

# haven't run for MaxMargin yet
remove = ["maxmargin", "friedman_rafsky"]
INDEP_TESTS = dict([(k, v) for k, v in INDEP_TESTS.items() if k not in remove])


def find_dim(sim):
    """Find dimension maximum for the simulation."""
    if sim not in SIMULATIONS.keys():
        raise ValueError("Invalid simulation")

    if sim in ["joint_normal", "sin_four_pi", "sin_sixteen_pi", "multiplicative_noise"]:
        dim = 10
    elif sim in ["multimodal_independence", "uncorrelated_bernoulli", "logarithmic"]:
        dim = 100
    elif sim in ["linear", "exponential", "cubic"]:
        dim = 1000
    elif sim in ["square", "diamond"]:
        dim = 40
    else:
        dim = 20

    return dim


def find_dim_range(dim):
    """Create list of dimension range to calculate power for."""
    if dim < 20:
        lim = 10
    else:
        lim = 20

    dim_range = list(range(int(dim / lim), dim + 1, int(dim / lim)))
    if int(dim / lim) != 1:
        dim_range.insert(0, 1)
    return dim_range


def estimate_power(sim, test, auto=False):
    """Compute the mean of the estimated power of 5 replications over sample sizes."""
    if test == "MaxMargin":
        test = ["MaxMargin", "Dcorr"]
    dim_range = find_dim_range(find_dim(sim))
    est_power = np.array(
        [
            np.mean(
                [
                    power(
                        test,
                        pow_type="indep",
                        sim=sim,
                        n=100,
                        p=dim,
                        auto=auto,
                        noise=True,
                    )
                    for _ in range(POWER_REPS)
                ]
            )
            for dim in dim_range
        ]
    )
    np.savetxt(
        "../benchmarks/vs_samplesize/{}_{}.csv".format(sim, test),
        est_power,
        delimiter=",",
    )

    return est_power


# At this point, we would run this bit of code to generate the data for the figure and
# store it under the "vs_sampsize" directory. Since this code takes a very long time,
# we have commented out these lines of codes. If you would like to generate the data,
# uncomment these lines and run the file.
#
# outputs = Parallel(n_jobs=-1, verbose=100)(
#     [
#         delayed(estimate_featimport)(sim_name, test)
#         for sim_name in SIMULATIONS.keys()
#         for test in INDEP_TESTS.keys()
#     ]
# )


def plot_power():
    fig, ax = plt.subplots(nrows=4, ncols=5, figsize=(25, 20))
    plt.suptitle(
        "Multivariate Independence Testing (Increasing Dimension)",
        y=0.93,
        va="baseline",
    )

    for i, row in enumerate(ax):
        for j, col in enumerate(row):
            count = 5 * i + j
            sim = list(SIMULATIONS.keys())[count]

            for test in INDEP_TESTS.keys():
                est_power = np.genfromtxt(
                    "../benchmarks/vs_dimension/{}_{}.csv".format(sim, test),
                    delimiter=",",
                )
                dim_range = find_dim_range(find_dim(sim))

                col.plot(dim_range, est_power, label=INDEP_TESTS[test].__name__, lw=2)
                col.set_xticks([])
                if i == 3:
                    col.set_xticks([dim_range[0], dim_range[-1]])
                col.set_ylim(-0.05, 1.05)
                col.set_yticks([])
                if j == 0:
                    col.set_yticks([0, 1])
                col.set_title(SIM_TITLES[count])

    fig.text(0.5, 0.05, "Dimension", ha="center")
    fig.text(
        0.07,
        0.5,
        "Statistical Power",
        va="center",
        rotation="vertical",
    )
    leg = plt.legend(
        bbox_to_anchor=(0.5, 0.05),
        bbox_transform=plt.gcf().transFigure,
        ncol=len(INDEP_TESTS.keys()),
        loc="upper center",
    )
    leg.get_frame().set_linewidth(0.0)
    for legobj in leg.legendHandles:
        legobj.set_linewidth(5.0)
    plt.subplots_adjust(hspace=0.50)


# plot the power
plot_power()

previous

Benchmarks

next

1D Independence Testing Power vs. Sample Size