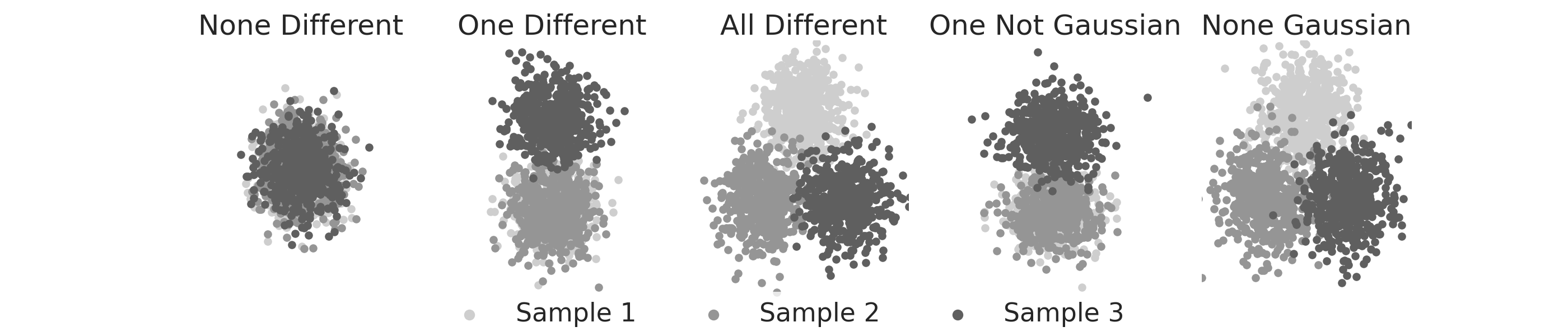
Guassian Sims

Gaussian k-sample simulations are found in hyppo.tools. Here, we visualize what these simulations look like. We use these Gaussian simulations when comparing our algorithms against multivariate analysis of variance (MANOVA).

import matplotlib.pyplot as plt
import seaborn as sns
from hyppo.tools import gaussian_3samp

# make plots look pretty
sns.set(color_codes=True, style="white", context="talk", font_scale=2)
PALETTE = sns.color_palette("Greys", n_colors=9)
sns.set_palette(PALETTE[2::2])

# constants
N = 500
CASES = [1, 2, 3, 4, 5]


# make a function to plot the Gaussian simulations
def plot_gaussian_sims():
    """Plot simulations"""
    fig, ax = plt.subplots(nrows=1, ncols=5, figsize=(28, 6))

    sim_titles = [
        "None Different",
        "One Different",
        "All Different",
        "One Not Gaussian",
        "None Gaussian",
    ]

    # plt.suptitle("Gaussian Simulations", y=0.93, va="baseline")

    for i, col in enumerate(ax):
        sim_title = sim_titles[i]

        # rotated k-sample simulation
        sims = gaussian_3samp(N, epsilon=4, weight=0.9, case=CASES[i])

        # plot the nose and noise-free sims
        for index in range(len(sims)):
            col.scatter(
                sims[index][:, 0],
                sims[index][:, 1],
                label="Sample {}".format(index + 1),
            )

        # make the plot look pretty
        col.set_title("{}".format(sim_title))
        col.set_xticks([])
        col.set_yticks([])
        col.set_xlim(-5, 5)
        if CASES[i] not in [2, 4]:
            col.set_ylim(-5, 5)
        sns.despine(left=True, bottom=True, right=True)

    leg = plt.legend(
        bbox_to_anchor=(0.5, 0.17),
        bbox_transform=plt.gcf().transFigure,
        ncol=3,
        loc="upper center",
    )
    leg.get_frame().set_linewidth(0.0)
    for legobj in leg.legend_handles:
        legobj.set_linewidth(5.0)
    plt.subplots_adjust(hspace=0.75)


# run the created function for the Gaussian simulations
plot_gaussian_sims()

previous

Independence Sims

next

K-Sample Sims