Overview

hyppo is a multivariate hypothesis testing package, dealing with problems such as independence testing, k-sample testing, time series independence testing, etc. It includes algorithms developed by the neurodata lab as well as relevant important tests within the field.

The primary motivation for creating hyppo was simply the limitations of tools that data scientists are afforded in Python, which then leads to complex workflows using other languages such as R or MATLAB. This is especially true for hypothesis testing, which is a very important part of data science.

Conventions

Before we get started, here are a few of the conventions we use within hyppo:

• All tests are releagted to a single class, and all classes have a test method. This method returns a test statistic and p-value, as well as other informative outputs depending on the test. We recommend using this method, though a statistic method exists that just returns the test statistic.

• All functions and classes accept numpy.ndarray as inputs. Optional inputs vary between tests within the package.

• Input data matrices have the shape (n, p) where n is the number of samples and p is the number of dimensions (or features)

The Library

Most classes and functions are available through the hyppo top level package, though our workflow generally involves importing specific classes or methods from our modules.

Our goal is to create a comprehensive hypothesis testing package in a simple and easy to use interface. Currently, we include the following modules: hyppo.independence, hyppo.ksample, hyppo.time_series, hyppo.discrim and hyppo.tools. The last of which does not contain any tests, but functions to generate simulated data, that we used to evalue our methods, as well as functions to calculate p-values or other important functions commmonly used between modules.

General Workflow

As an example, let's generate some simulated data using hyppo.tools.w_shaped:

from hyppo.tools import w_shaped

# 100 samples, 1D x and 1D y, noise
x, y = w_shaped(n=100, p=1, noise=True)

The data are points simulating a noisy spiral relationship between random variables \(X\) and \(Y\) and returns realizations as numpy.ndarray:

import matplotlib.pyplot as plt
import seaborn as sns

# make plots look pretty
sns.set(color_codes=True, style="white", context="talk", font_scale=1)

# look at the simulation
plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.xticks([])
plt.yticks([])
sns.despine(left=True, bottom=True, right=True)
plt.show()

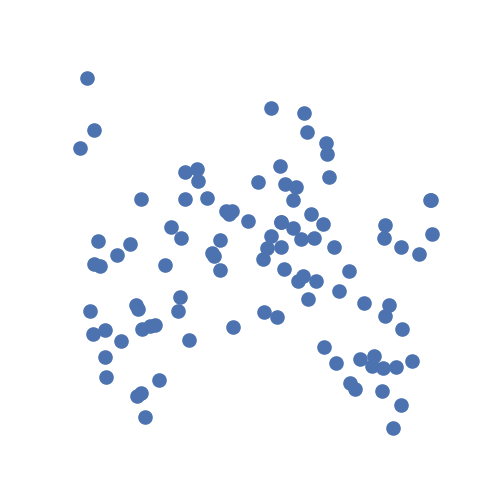
Let's ask the question: are x and y independent? From the description given above, the answer to that is obviously no. From the simulation visualization, it's hard to tell. We can verify whether or not we can see a trend within the data by running an independence test. Let's use the test multiscale graph correlation (MGC) which, as an aside, was the test that started the creation of the package. We have to import it, and then run the test.

First, we initalize the class. Most tests have a compute_distance parameter that can use accept any metric from sklearn.metric.pairwise_distances (or sklearn.metrics.pairwise.pairwise_kernels for kernel-based methods) and additional keyword arguments for the method. The parameter can also accept a custom function, or None in the case where the inputs are already distance matrices.

Each test also has a test method that has a reps parameter that controls the replications of hyppo.tools.perm_test and the workers parameter controls the number of threads when running the parallelized code (-1 uses all available cores). We highly recommend using a number >= 1 in general since speed increases are noticeable.

from hyppo.independence import MGC

stat, pvalue, mgc_dict = MGC().test(x, y)
print(stat, pvalue)

Out:

0.1130219549131264 0.001998001998001998

Note: MGC, like some tests, have 3 outputs. In general, tests in hyppo.independence have 2 outputs.

We see that we are right! Since the p-value is less than the alpha level of 0.05, we can conclude that random variables \(X\) and \(Y\) are dependent (and reject the null hypothesis that they are independent). And that's it!

Wrap Up

This covers the basics of using most tests in hyppo. Most use cases and examples in the documentation will involve some variation of the following workflow:

1. Load your data and convert to numpy.ndarray

2. Import the desired test

3. Run the test on your data

4. Obtain a test statistic and p-value (among other outputs)

previous

Installing

next

Citing hyppo